И«өИДЈРНЦ®Иэҙ№Цұ����ЎўИэөИҪЗДЈРН
Иэҙ№Цұ��ЎўИэөИҪЗДЈРН
¶ЁБxЈәИэӮҖ(gЁЁ)өИҪЗөДн”ьc(diЁЈn)ФЪН¬Т»—lЦұҫҖЙПҳӢ(gЁ°u)іЙөДҲDРО�Ј¬Я@ӮҖ(gЁЁ)ҪЗҝЙТФКЗЦұҪЗЈ¬ТІҝЙТФКЗдJҪЗ»твgҪЗ��Ј¬Т»°гКЗТФөИСьИэҪЗРО»тХЯөИЯ…ИэҪЗРОһйұіҫ°����ЎЈЯ@ӮҖ(gЁЁ)ДЈРНШһҙ©іхЦРҺЧәОөДКјҪK�Ј¬іхИэЦvЎ¶ПаЛЖИэҪЗРОЎ·•r(shЁӘ)Я@ТІКЗТ»ӮҖ(gЁЁ)·ЗіЈЦШТӘөДЦӘЧR(shЁӘ)ьc(diЁЈn)
·Ҫ·ЁМбҹ’
1 Ифо}ДҝЦРУРТ»ҫҖИэ(ЦұҪЗ)өИҪЗ�����Ј¬ҝЙТФЦұҪУЧCГчПаЛЖ»тИ«өИҢҚ(shЁӘ)¬F(xiЁӨn)Я…ЕcҪЗөДЮD(zhuЁЈn)»Ҝ;
2 Ифо}ДҝЦРӣ](mЁҰi)УРҪoіцТ»ҫҖИэ(ЦұҪЗ)өИҪЗ����Ј¬ҝЙТФёщ“ю(jЁҙ)РиТӘҒн(lЁўi)ҳӢ(gЁ°u)Фм
»щұҫДЈРНЈә(1)Т»ҫҖИэҙ№Цұ
Ўҫ»щұҫҲDРОЎҝ
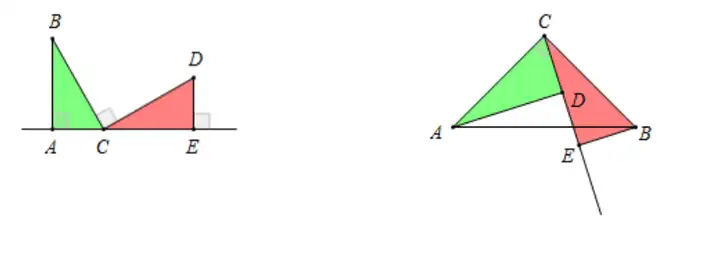
И«өИДЈРНЦ®°лҪЗДЈРН
¶ЁБxЈәҠA°лҪЗЈ¬оҷГыЛјБx�����Ј¬КЗТ»ӮҖ(gЁЁ)ҙуҪЗҠAЦшТ»ӮҖ(gЁЁ)ҙуРЎЦ»УРЖдТ»°лөДҪЗ����Ј¬ИзПВҲDЛщКҫ����ЎЈ
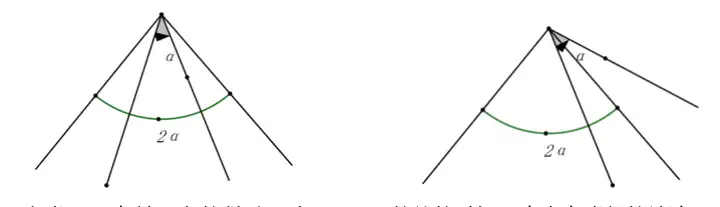
Я@оҗо}ДҝУРЖд№М¶ЁөДЧц·ЁЈ¬®”(dЁЎng)aИЎІ»Н¬өДЦөөД•r(shЁӘ)әт���Ј¬ТІ•ю(huЁ¬)УРоҗЛЖөДҪY(jiЁҰ)Х“
ҠA°лҪЗөДіЈТҠ(jiЁӨn)·ЦоҗЈә
(1)90 ¶ИҠA 45 ¶И
(2)120 ¶ИҠA 60 ¶И
(3)2αҠAα
о}РНТ» 90 ¶ИҠA 45 ¶И
ЎҫАэ 1Ўҝ ИзҲD���Ј¬Хэ·ҪРОABCD ЦР���Ј¬EФЪBCЙПЈ¬F(xiЁӨn)ФЪCDЙП�����Ј¬ЗТ∠EAF=45°�Ј¬ЗуЧCЈә(1)BE+DF=EF
(2)∠AEB=∠AEF
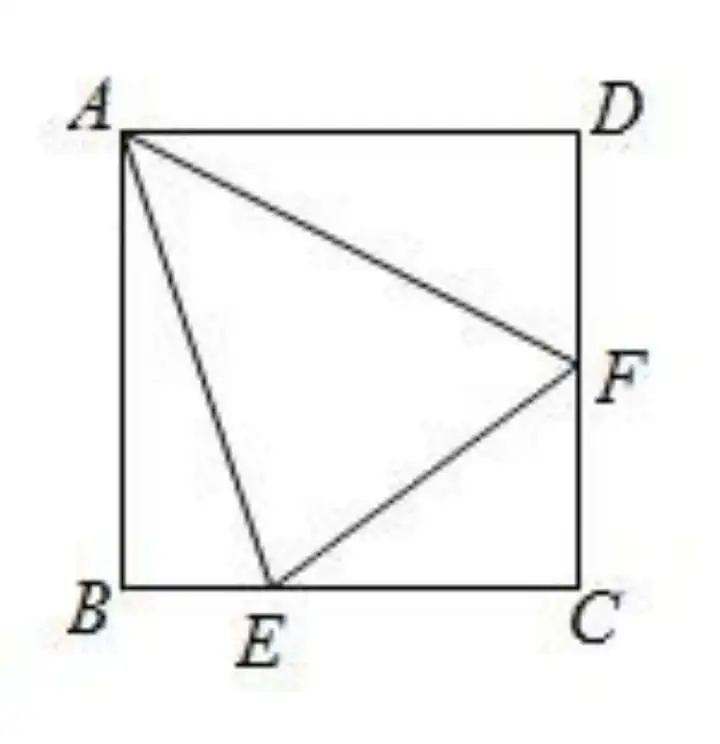
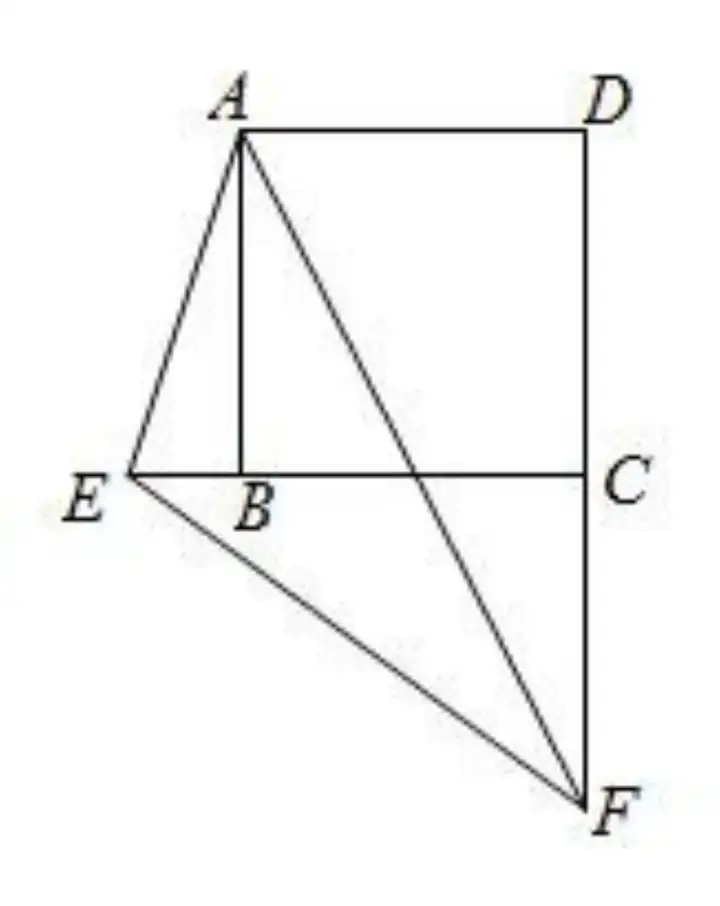
(2)ФЪАэ 1 өД—lјюПВЈ¬ИфEФЪCBСУйL(zhЁЈng)ҫҖЙП����Ј¬F(xiЁӨn)ФЪDCСУйL(zhЁЈng)ҫҖЙПЈ¬ЖдУа—lјюІ»Чғ�����Ј¬ЧCГчЈә
(1)DF-BE=EF
(2)∠AEB+∠AEF=180°
ЦРьc(diЁЈn)ДЈРН
ДЈРН1.ұ¶йL(zhЁЈng)ЦРҫҖ»тоҗЦРҫҖ(ЕcЦРьc(diЁЈn)УРкP(guЁЎn)өДҫҖ¶О)ҳӢ(gЁ°u)ФмИ«өИИэҪЗРО
ИзҲDўЩ�����Ј¬ADКЗЎчABCөДЦРҫҖ�Ј¬СУйL(zhЁЈng)ADЦБьc(diЁЈn)EК№DE=ADЈ¬ТЧЧCЈәЎчADCЎХEDB(SAS)���ЎЈ
ИзҲDўЪ��Ј¬DКЗBCЦРьc(diЁЈn)�����Ј¬СУйL(zhЁЈng)FDЦБьc(diЁЈn)EК№DE=FD��Ј¬ТЧЧCЈәЎчFDBЎХЎчEDC(SAS)��ЎЈ
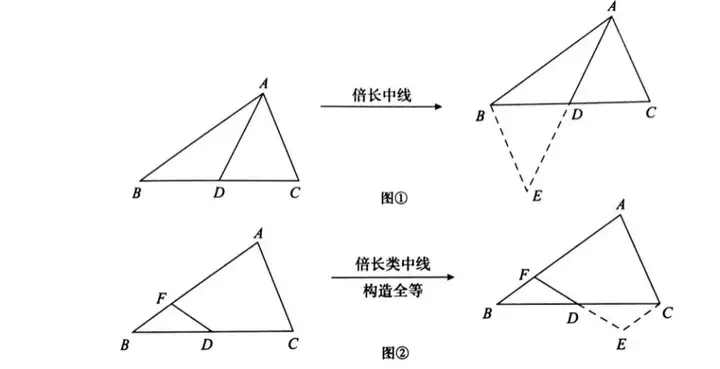
ДЈРН·ЦОцЈә
®”(dЁЎng)УцТҠ(jiЁӨn)ЦРҫҖ»тХЯЦРьc(diЁЈn)өД•r(shЁӘ)әт����Ј¬ҝЙТФҮLФҮұ¶йL(zhЁЈng)ЦРҫҖ»тұ¶йL(zhЁЈng)оҗЦРҫҖЈ¬ҳӢ(gЁ°u)ФмИ«өИИэҪЗРО�Ј¬ДҝөДКЗҢҰ(duЁ¬)ТСЦӘ—lјюЦРөДҫҖ¶ОЯM(jЁ¬n)РРЮD(zhuЁЈn)ТЖ�����ЎЈ
Аэ1. ИзҲD��Ј¬ТСЦӘФЪЎчABCЦР����Ј¬ADКЗBCЯ…ЙПөДЦРҫҖЈ¬EКЗADЙПТ»ьc(diЁЈn)�Ј¬ЯBҪУBEІўСУйL(zhЁЈng)Ҫ»ACУЪьc(diЁЈn)F����Ј¬AF=EF�����ЎЈЗуЧCЈәAC=BE���ЎЈ
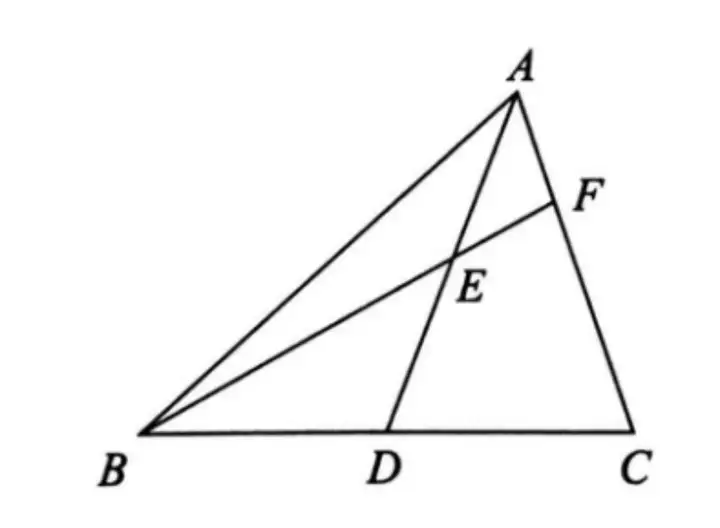
ДЈРН2.ТСЦӘөИСьИэҪЗРОөЧЯ…ЦРьc(diЁЈn)���Ј¬ҝЙТФҝј‘]Еcн”ьc(diЁЈn)ЯBҪУУГ“ИэҫҖәПТ»”
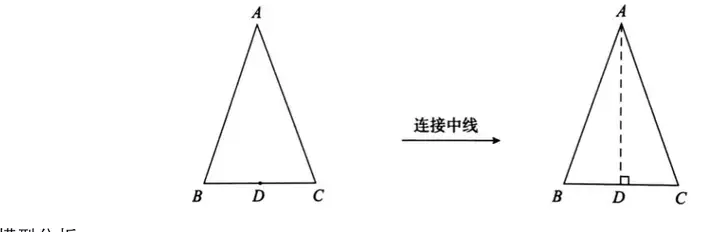
ДЈРН·ЦОцЈә
өИСьИэҪЗРОУРөЧЯ…ЦРьc(diЁЈn)•r(shЁӘ)Ј¬іЈЧчөЧЯ…өДЦРҫҖ���Ј¬АыУГөИСьИэҪЗРО“ИэҫҖәПТ»”өДРФЩ|(zhЁ¬)өГөҪҪЗПаөИ»тЯ…ПаөИ���ЎЈһйҪво}„“(chuЁӨng)Фмёь¶аөД—lјюЈ¬®”(dЁЎng)ҝҙөҪөИСьИэҪЗРОөД•r(shЁӘ)әт����Ј¬ҫН‘Ә(yЁ©ng)ПлөҪ“Я…өИЎўҪЗөИ����ЎўИэҫҖәПТ»”�����ЎЈ
Аэ.ИзҲD�Ј¬ФЪЎчABCЦР��Ј¬AB=AC=5�Ј¬BC=6Ј¬MһйBCөДЦРьc(diЁЈn)��Ј¬MN⊥ACУЪьc(diЁЈn)N����Ј¬ЗуMNөДйL(zhЁЈng)¶ИЎЈ
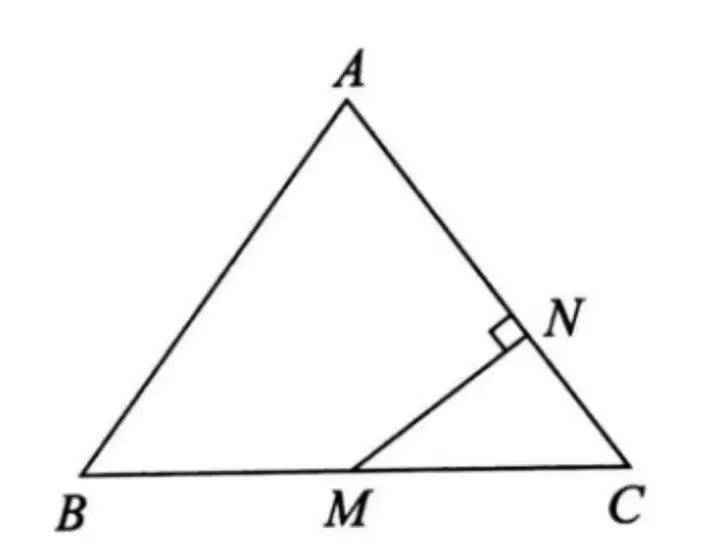
ДЈРН3.ТСЦӘИэҪЗРОТ»Я…өДЦРьc(diЁЈn)��Ј¬ҝЙТФҝј‘]ЦРО»ҫҖ¶ЁАн

ДЈРН·ЦОцЈә
ФЪИэҪЗРОЦР���Ј¬Из№ыУРЦРьc(diЁЈn)Ј¬ҝЙҳӢ(gЁ°u)ФмИэҪЗРОөДЦРО»ҫҖ�����Ј¬АыУГИэҪЗРОЦРО»ҫҖөДРФЩ|(zhЁ¬)¶ЁАнЈәDEЎОBC����Ј¬ЗТDE=1/2BCҒн(lЁўi)Ҫво}��ЎЈЦРО»ҫҖ¶ЁАнЦРјИУРҫҖ¶ОЦ®йgөДО»ЦГкP(guЁЎn)ПөУЦУР”ө(shЁҙ)БҝкP(guЁЎn)Пө�Ј¬Ф“ДЈРНҝЙТФҪвӣQҪЗПаөИ���Ј¬ҫҖ¶ОЦ®йgөДұ¶°л����ЎўПаөИј°ЖҪРРҶ–(wЁЁn)о}���ЎЈ
Аэ. ФЪЛДЯ…РОABCDЦР�����Ј¬AB=CD�����Ј¬E�����ЎўF·Ц„eКЗBC�����ЎўADөДЦРьc(diЁЈn)��Ј¬ЯBҪУEFІўСУйL(zhЁЈng)���Ј¬·Ц„eЕcBA�ЎўCDөДСУйL(zhЁЈng)ҫҖҪ»УЪьc(diЁЈn)M�����ЎўN��ЎЈЗуЧCЈә∠BME=∠CNE�����ЎЈ
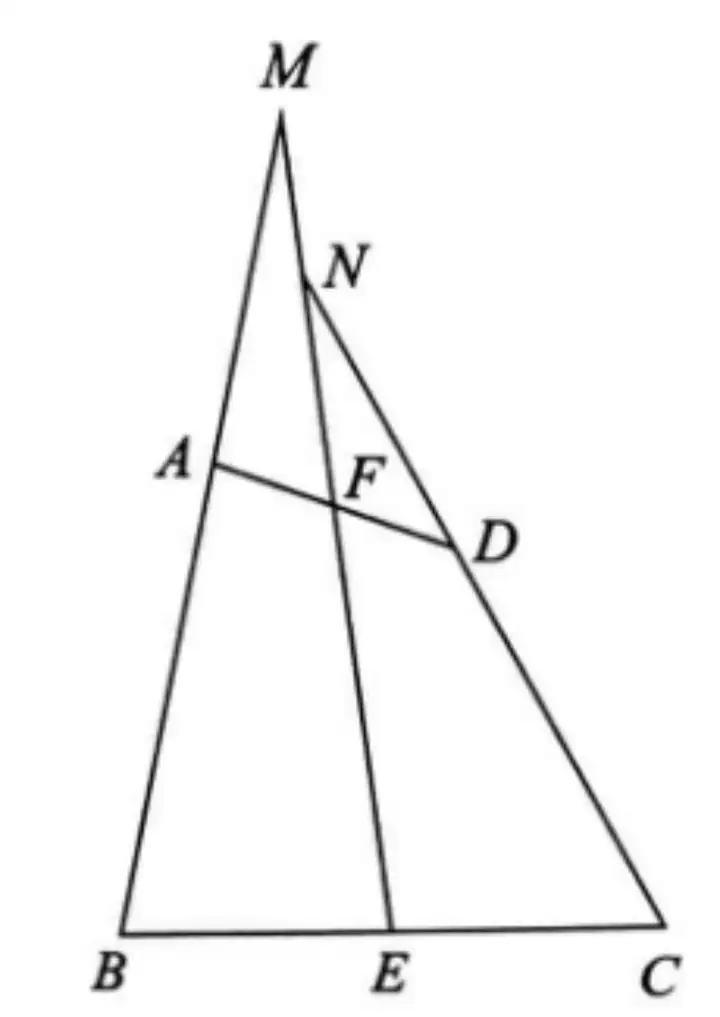
ДЈРН4.ТСЦӘЦұҪЗИэҪЗРОРұЯ…ЦРьc(diЁЈn)�Ј¬ҝЙТФҝј‘]ҳӢ(gЁ°u)ФмРұЯ…ЦРҫҖ

ДЈРН·ЦОцЈә
ФЪЦұҪЗИэҪЗРОЦРЈ¬®”(dЁЎng)УцТҠ(jiЁӨn)РұЯ…ЦРьc(diЁЈn)•r(shЁӘ)����Ј¬Ҫӣ(jЁ©ng)іЈ•ю(huЁ¬)ЧчРұЯ…ЙПөДЦРҫҖЈ¬АыУГЦұҪЗИэҪЗРОРұЯ…ЙПөДЦРҫҖөИУЪРұЯ…өДТ»°л����Ј¬јҙCD=1/2ABЈ¬Ғн(lЁўi)ЧCГчҫҖ¶ОйgөД”ө(shЁҙ)БҝкP(guЁЎn)Пө�����Ј¬¶шЗТҝЙТФөГөҪғЙӮҖ(gЁЁ)өИСьИэҪЗРОЈәЎчACDәНЎчBCD����Ј¬Ф“ДЈРНҪӣ(jЁ©ng)іЈ•ю(huЁ¬)ЕcЦРО»ҫҖ¶ЁАнТ»ЖрҫCәП‘Ә(yЁ©ng)УГЎЈ
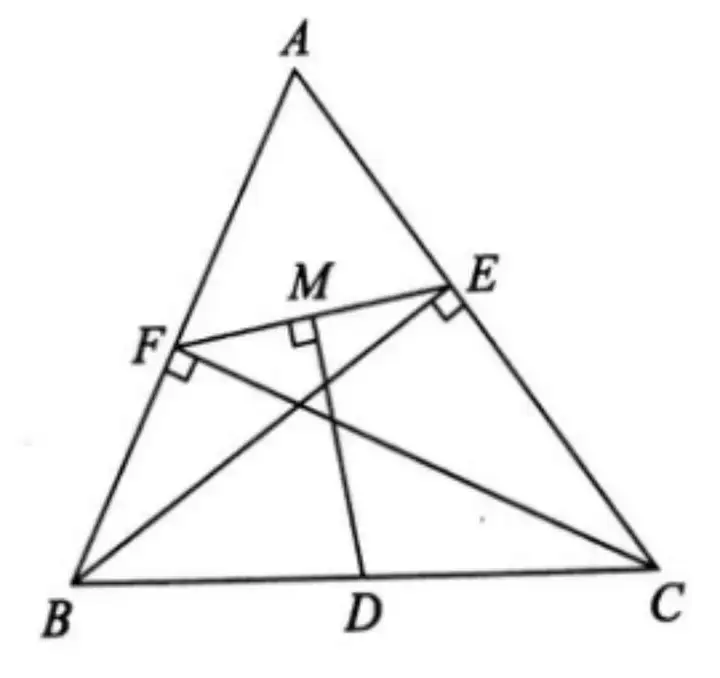
Аэ. ИзҲD�����Ј¬ФЪЎчABCЦР�Ј¬BEЎўCF·Ц„eһйAC����ЎўABЙПөДёЯЈ¬DһйBCөДЦРьc(diЁЈn)�Ј¬DM⊥EFУЪьc(diЁЈn)MЎЈЗуЧCЈәFM=EM����ЎЈ
КЦАӯКЦДЈРН
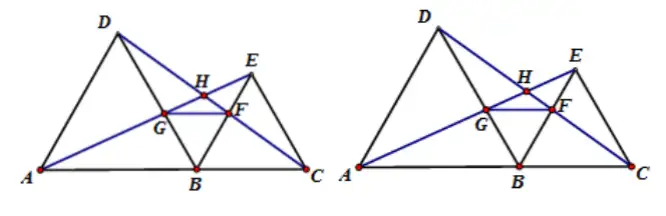
Аэ1���ЎўФЪЦұҫҖABCөДН¬Т»ӮИ(cЁЁ)ЧчғЙӮҖ(gЁЁ)өИЯ…ИэҪЗРОЎчABDәНЎчBCEЈ¬ЯBҪУAEЕcCD���Ј¬ЧCГчЈә
(1) ЎчABEЎХЎчDBC
(2) AE=DC
(3) AEЕcDCөДҠAҪЗһй60�����ЎЈ
(4) ЎчAGBЎХЎчDFB
(5) ЎчEGBЎХЎчCFB
(6) BHЖҪ·Ц∠AHC
(7) GFЎОAC
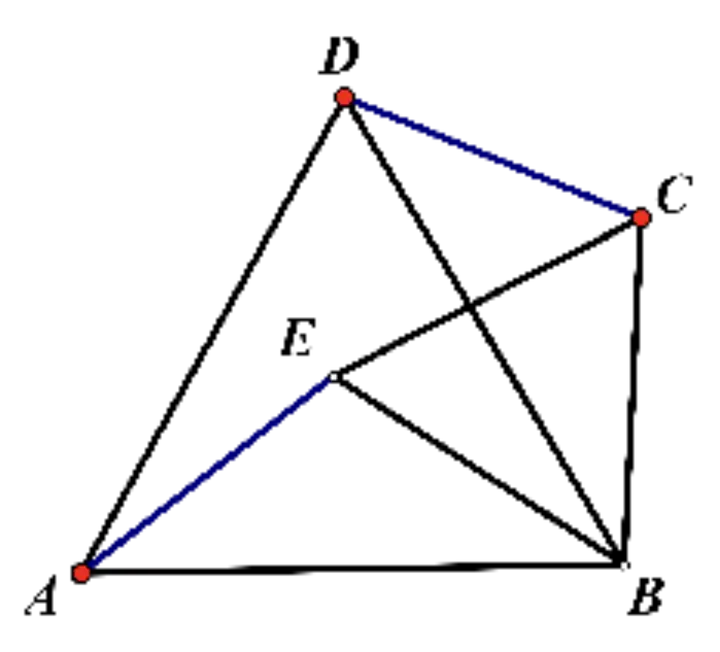
ЧғКҪҫҡБ•(xЁӘ)1����ЎўИз№ығЙӮҖ(gЁЁ)өИЯ…ИэҪЗРОЎчABDәНЎчBCE���Ј¬ЯBҪУAEЕcCD��Ј¬ЧCГчЈә
(1) ЎчABEЎХЎчDBC
(2) AE=DC
(3) AEЕcDCөДҠAҪЗһй60�ЎЈ
(4) AEЕcDCөДҪ»ьc(diЁЈn)ФO(shЁЁ)һйH,BHЖҪ·Ц∠AHC
ұјсYДЈРН
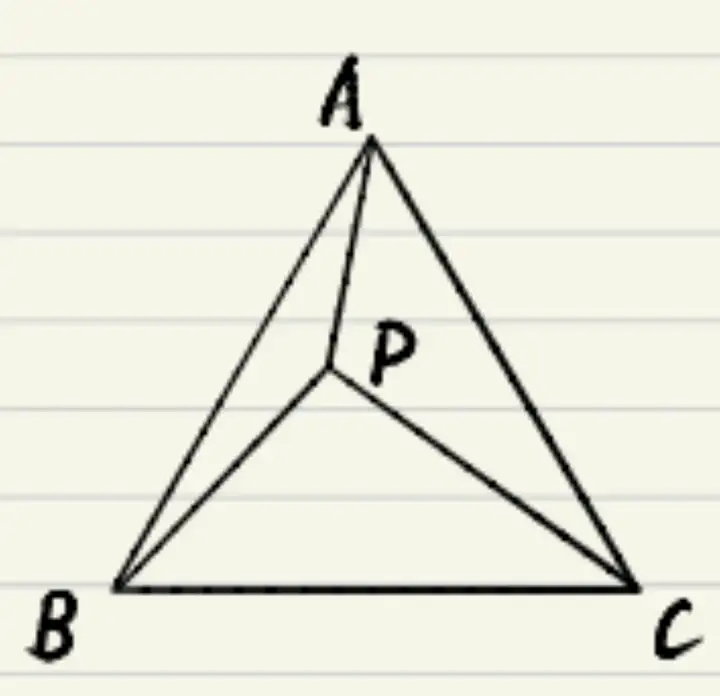
ҪШйL(zhЁЈng)Сa(bЁі)¶М
ҪШйL(zhЁЈng)Сa(bЁі)¶М·ЁҳӢ(gЁ°u)ФмИ«өИИэҪЗРО
ҪШйL(zhЁЈng)Сa(bЁі)¶М·Ё����Ј¬КЗіхЦР”ө(shЁҙ)ҢW(xuЁҰ)ҺЧәОо}ЦРТ»·NЭoЦъҫҖөДМнјУ·Ҫ·ЁЈ¬ТІКЗ°СҺЧәОо}»ҜлyһйТЧөДТ»·NЛјПл.ЛщЦ^“ҪШйL(zhЁЈng)”���Ј¬ҫНКЗҢўИэХЯЦРЧойL(zhЁЈng)өДДЗ—lҫҖ¶ОТ»·Цһй¶ю��Ј¬К№ЖдЦРөДТ»—lҫҖ¶ОөИУЪТСЦӘөДғЙ—lЭ^¶МҫҖ¶ОЦРөДТ»—l��Ј¬И»әуЧCГчЖдЦРөДБнТ»¶ОЕcТСЦӘөДБнТ»—lҫҖ¶ОПаөИ;ЛщЦ^“Сa(bЁі)¶М”�����Ј¬ҫНКЗҢўТ»ӮҖ(gЁЁ)ТСЦӘөДЭ^¶МөДҫҖ¶ОСУйL(zhЁЈng)ЦБЕcБнТ»ӮҖ(gЁЁ)ТСЦӘөДЭ^¶МөДйL(zhЁЈng)¶ИПаөИ�����Ј¬И»әуЗуіцСУйL(zhЁЈng)әуөДҫҖ¶ОЕcЧойL(zhЁЈng)өДТСЦӘҫҖ¶ОөДкP(guЁЎn)Пө.УРөДКЗІЙИЎҪШйL(zhЁЈng)Сa(bЁі)¶Мәу���Ј¬К№Ц®ҳӢ(gЁ°u)іЙДі·NМШ¶ЁөДИэҪЗРОЯM(jЁ¬n)РРЗуҪв.
ҪШйL(zhЁЈng)Сa(bЁі)¶М·ЁЧчЭoЦъҫҖЈ¬ЯmәПУЪЧCГчҫҖ¶ОөДәН����ЎўІоЎўұ¶���Ўў·ЦөИоҗөДо}Дҝ.

ЎЎЎЎ ҡgУӯК№УГКЦҷC(jЁ©)�����ЎўЖҪ°еөИТЖ„У(dЁ°ng)ФO(shЁЁ)ӮдФLҶ–(wЁЁn)ЦРҝјҫW(wЁЈng)����Ј¬2023ЦРҝјТ»В·Ег°йН¬РРЈЎ>>ьc(diЁЈn)“фІйҝҙ

























